February 2021

Este artigo foi escrito para o trabalho final da Unidade Curricular de Computação Estatística em R do Mestrado de Biometria e Bioestatística da Universidade Aberta. O trabalho tinha como tema “Simulação em Inferência Estatística”. 

O prazo era bastante apertado, e imaginar e desenvolver um tema com pés e cabeça foi um desafio. Quando me aproximei do fim vi que tinha delineado algumas ideias pouco interessantes, mas não havia para alterar. Isso levou a que o trabalho ficasse com alguns objectivos totós o que acabou em alguns resultados totós.  Mas apesar disso foi interessante de desenvolver e aprendi bastante. .

Para simular a possibilidade de implementar estufas com explorações agrícolas regadas apenas com água da chuva, decidiu-se aproveitar parte da área ardida do pinhal de Leira para executar uma série de experiências. A água disponível é a única variável a considerar para a área a plantar e neste trabalho pretende-se calcular essa área recorrendo aos dados de pluviosidade disponibilizados pelo IPMA para efectuar as simulações.

Com o objectivo de testar explorações agrícolas que só dependam da água da chuva em condições bastante específicas e limitadas foi implementada a seguinte experiência:

A base para as simulações feitas foi a base de dados do IPMA com medições de pluviosidade para o país inteiro entre 1950 e 2003 [2]. Foram isolados os registos referente a São Pedro de Moel e disponibilizados para acesso mais simples em:

http://paginasavulsas.claudiotereso.com/mbb/CE_R/precipitacao_s_pedro_moel.csv.

O primeiro passo é escolher o mês extra a usar para recolher água analisando a precipitação média por mês durante os anos disponíveis:

Listagem 1: Leitura e visualização dos dados

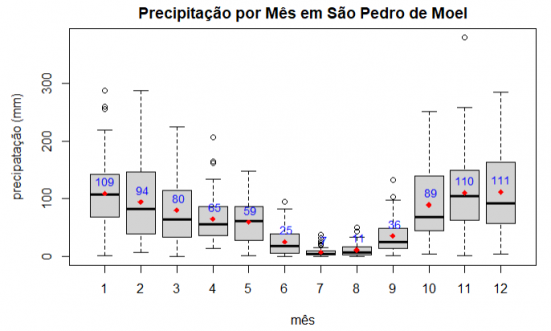
Gráfico 1: Diagrama de caixa da precipitação por mês

Os meses em que mais choveu foram, por ordem decrescente, Dezembro, Novembro e Janeiro. Os valores são muito semelhantes, mas só podemos escolher um, por isso vamos avançar com Dezembro que tem a média mais elevada, apesar de ser o que apresenta maior variação, com a segurança de que, se houver problemas para efectuar a recolha e Dezembro, Novembro e Janeiro serão bons substitutos.

Com os dados escolhidos, precisamos de analisar a sua distribuição para podermos efectuar a sua simulação. Podemos ver no Gráfico 2 o histograma da densidade para Agosto e Dezembro.

 

Gráfico 2: Histogramas da precipitação

Para obter a função distribuição a partir de um conjunto de dados, existem em R várias bibliotecas disponíveis [3]. Depois de vários testes optou-se pela simukde [4] que apresentou resultados bastante satisfatórios e de fácil interpretação.

# Carrega biblioteca simukde
if(!require(simukde)) {install.packages(“simukde”);require(simukde)}

# Obtem subconjunto para cada um dos meses
agosto<-subset(precipitacaoSPedroMoel,precipitacaoSPedroMoel$mes==’8′)$precip
dezembro<-subset(precipitacaoSPedroMoel,precipitacaoSPedroMoel$mes==’12’)$precip

# há meses com 0 o que invalida o uso da função find_best_fit, aumentamos todos 0,01
agosto<-agosto+0.01

# Verifica ajustamento dos dados com distribuições teóricas
distAgosto<-find_best_fit(agosto,positive = TRUE)
distDezembro<-find_best_fit(dezembro,positive = TRUE)

Listagem 3: Obtenção de distribuçãoes para os dados

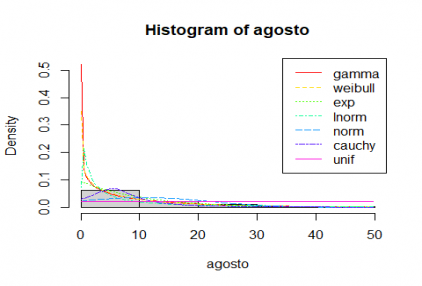
Gráfico 3: Comparação de precipitação de Agosto com distribuições teóricas

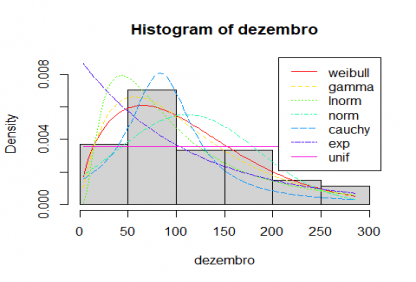
Gráfico 4: Comparação de precipitação de Dezembro com distribuições teóricas

A função find_best_fit compara os dados com várias distribuições e apresenta essas distribuições pela ordem que melhor se ajusta à distribuição analisada. Os resultados indicam que para Agosto devemos usar uma distribuição gamma e para Dezembro uma distribuição weibull. No entanto não nos são dados os parâmetros da função a usar, informação que podemos obter com a função fitdist da biblioteca fitdistrplus [5]:

.

# Carrega bibliotecas fitdostrplus e knirt que é usada para apresentar dados em tabela
if(!require(fitdistrplus)) {install.packages(“fitdistrplus”);require(fitdistrplus)}
if(!require(knitr)) {install.packages(“knitr”);require(knitr)}

# Obtem parâmetros das distribuições
fitAgosto <- fitdist(agosto,distr=”gamma”)
fitDezembro <- fitdist(dezembro,distr=”weibull”)

# Apresenta resultados

kable(fitAgosto$estimate,caption = “Agosto, parâmetros para distribuição gamma”)
kable(fitDezembro$estimate,caption = “Dezembro, parâmetros para distribuição weibull”)

Listagem 4: Obter parâmetros das distribuições

.
shape	0.6738999
rate	0.0633861

Tabela 1: Agosto, parâmetros para distribuição gamma

.
shape	1.567725
scale	124.040283

Tabela 2: Dezembro, parâmetros para distribuição weibull

Temos agora todos os dados que precisamos para simular a precipitação em Agosto e Dezembro, mas vamos antes confirmar se os nossos simuladores calculados são fidedignos. Primeiro visualmente:

# Prepara para mostrar dois gráficos simultameneamente
par(mfrow=c(1,2))

# Histogramas de quantidade de precipitação e distribuição teórica para Agosto
hist(subset(precipitacaoSPedroMoel,precipitacaoSPedroMoel$mes==’8′)$precip,
freq = FALSE,main=”Agosto”,xlab=”Precipitação (mm)”)
curve(dgamma(x,shape=0.6738999,rate=0.0633861),add=TRUE)

# Histogramas de quantidade de precipitação e distribuição teórica para Dezembro
hist(subset(precipitacaoSPedroMoel,precipitacaoSPedroMoel$mes==’12’)$precip,
freq = FALSE,main=”Dezembro”,xlab=”Precipitação (mm)”)
curve(dweibull(x,shape=1.567725,scale=124.040283),add=TRUE)

Listagem 5: Histogramas e distribuições teóricas

Gráfico 5: Histogramas e distribuições teóricas

.

As funções aparentam simular bem as distribuições dos dados, mas vamos ver mais ao pormenor:

# Inicializa geração de números aleatórios
set.seed(0)

# Compara dados de Agosto com distribuição teórica
amostraDistGama<-rgamma(100000,shape=0.6738999,rate=0.0633861)
sprintf(“Agosto – Médias : %7.3f, %7.3f”,mean(amostraDistGama),mean(agosto))
## [1] “Agosto – Médias : 10.666, 10.632”
sprintf(“Agosto – D Padrão : %f, %f”,sd(amostraDistGama),sd(agosto))
## [1] “Agosto – D Padrão : 13.022360, 11.294285”

# Compara dados de Dezembro com distribuição teórica
amostraDistRweibull <- rweibull(100000,shape=1.567725,scale=124.040283)
sprintf(“Dezembro – Médias : %f, %f”,mean(amostraDistRweibull),mean(dezembro))
## [1] “Dezembro – Médias : 111.803654, 111.442222”
sprintf(“Dezembro – D Padrão : %f, %f”,sd(amostraDistRweibull),sd(dezembro))
## [1] “Dezembro – D Padrão : 72.744649, 72.887143”

Listagem 6: Comparação de dados com distribuições teóricas

.	Média	D. Padrão	Média	D. Padrão
Simulação	10.67	13.02	111.8	72.74
Dados	10.62	11.29	111.4	72.89

Listagem 7: Comparação de dados com distribuições teóricas

Como podemos verificar, a média e desvio padrão das funções de distribuição são praticamente coincidentes com os dados reais, pelo que podemos considerar que temos condições para avançar para a simulação.

Precisamos agora de fazer as simulações desejadas. Essa tarefa é composta por dois passos, construir as funções para executar as simulações e as simulações propriamente ditas.

Iniciamos os nossos cálculos com a construção de uma função para simular a água disponível para cada ano:

aguaDisponivel <- function(area) # area em metros quadrados
{
# Gera uma observação aleatória para Agosto
  chuvaAgosto<-rgamma(1,shape=0.6738999,rate=0.0633861)
# Gera uma observação aleatória para Dezembro
  chuvaDezembro<-rweibull(1,shape=1.567725,scale=124.040283)
# Calcula total água obtida
  return((chuvaAgosto+chuvaDezembro)*area)
}

Listagem 8: Função “aguaDisponivel”

A função simula a pluviosidade segundo a distribuição para Agosto e Dezembro e multiplica pelos metros quadrados da área onde a chuva cai. Como um milímetro de altura por metro quadrado equivale a um litro, o resultado da multiplicação devolve o resultado em litros.

Pretendemos, para um determinado período, obter os valores de pluviosidade dos anos menos e mais chuvosos de cada série para dimensionarmos a área a plantar. É esse o objectivo da função seguinte:

chuvaAnualMinimoMaximo <- function(area,anos) # area em metros quadrados
{
# Incializa maximo e minimo com valores extremos
  maximo <-0
  minimo <- 1000000

# Faz simulação para os anos indicados
  for (i in 1:anos) {
# Faz uma simulação
    aguaAnoActual<-aguaDisponivel(area)
# Verifica se minimo e máximo foram ultrapassados e actualiza se for o caso
    maximo <- max(maximo,aguaAnoActual)
    minimo <- min(minimo,aguaAnoActual)
}
# Devolve minimo e máximo obtidos
  return(c(minimo,maximo))
}

Listagem 9: Função “chuvaAnualMinimoMaximo”

Já temos as funções necessárias para fazer as simulações. Vamos fazer 100 mil simulações para um período de 20 anos e vamos analisar a chuva anual mínima e máxima em cada uma dessas séries.

# Inicializa geração de números aleatórios
set.seed(0)
# Executa 100 000 simulações
num_simulacoes <- 100000
simulacoes <- sapply(1:num_simulacoes,function(x) chuvaAnualMinimoMaximo(100,20))

# Faz histogramas de valores obtidos
hist(simulacoes[1,],xlim=c(0,50000),freq=FALSE,breaks=50,
main=”Distribuição dos melhores e piores anos em cada série”,xlab=”precipitação (mm)”)
hist(simulacoes[2,],add=TRUE,freq=FALSE,breaks=100)

Listagem 10: Simulações para 20 anos

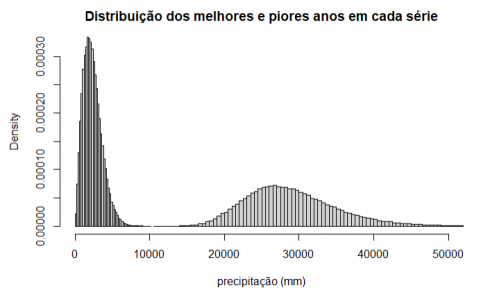
Gráfico 6: Histogramas de melhores e piores anos em cada série

Os valores das médias e dos desvios padrão são:

sprintf(“Mínimo -> Média: %.2f, D.Padrão: %.2f”,mean(simulacoes[1,]),sd(simulacoes[1,]))
## [1] “Mínimo -> Média: 2345.46, D.Padrão: 1243.67”

sprintf(“Máximo -> Média: %.2f, D.Padrão: %.2f”,mean(simulacoes[2,]),sd(simulacoes[2,]))
## [1] “Máximo -> Média: 28933.78, D.Padrão: 6080.94”

Listagem 11: Médias e Desvios Padrão

Podemos verificar que as distribuições obtidas têm uma distribuição a tender para a normal, o que podemos verificar sobrepondo a distribuição normal teórica com médias e desvios padrão dos valores obtidos:

curve(dnorm(x,mean=mean(simulacoes[1,]),sd(simulacoes[1,])),add=TRUE,col = “red”)
curve(dnorm(x,mean=mean(simulacoes[2,]),sd(simulacoes[2,])),add=TRUE,col = “red”)

Listagem 12: Adicionar Distribuições normais aos histogramas

.

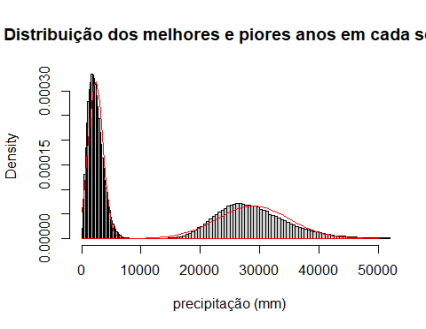
Gráfico 7: Histogramas e distribuição normal de melhores e piores anos em cada série

Queremos agora obter valores que nos permitam com alguma garantia que não nos vai faltar água para colheitas Tipo I e perceber quantas Tipo II devemos plantar.

Comecemos pelas colheitas Tipo I. Na nossa amostra, o mínimo de água disponível é em média 2 345 litros. Vamos usar a distribuição normal, para obter valores para diversas probabilidades de pluviosidade mínima:

# Probabilidades a verificar: 5%, 10%, 20%
probTesteMin <- c(0.05,0.1,0.2)
# Obter pluviosidade para as probabilidades indicadas
qnorm(probTesteMin,mean(simulacoes[1,]),sd(simulacoes[1,]))
## [1] 299.8136 751.6406 1298.7676
.

# Estufas Tipo I possível para as probabilidades indicadas
qnorm(probTesteMin,mean(simulacoes[1,]),sd(simulacoes[1,]))/31/5
## [1] 1.934282 4.849294 8.379146

Listagem 13: Cálculo de probabilidade de pluviosidade

Devido ao custo das plantações Tipo I, o ideal seria correr apenas um risco de cinco por cento de não ter água suficiente para as estufas, mas isso só nos dá 2 estufas, o que é manifestamente pouco, como tal foi decidido arriscar o limite dos 10% e montar 5 estufas.

Quanto ao Tipo II, para equilibrar o potencial desperdício de água com a potencial perda de colheita decidiu-se avançar com a média dos anos melhores, que foi de aproximadamente 29 mil litros. As Estufas Tipo I vão-nos gastar 775 litros, sobram-nos pouco mais de 28 mil litros, o que dá para cerca de 18 estufas Tipo II.

A decisão final foi de montar 5 estufas Tipo I e 18 estufas Tipo II.

A decisão foi tomada de um modo orgânico, inicialmente estava pensado usar o limite dos 5% de probabilidade de pluviosidade mínima para o limite das estufas Tipo I, mas isso revelou-se demasiado baixo. A utilização dos 10% é aceitável, desde que o risco extra que se está a correr seja compreendido por todos os envolvidos.

Quanto às estufas de Tipo II, seriam precisos mais dados sobre os custos de perder colheita para poder optar por um limite diferente. Sem essa informação parece-nos razoável apostar numa probabilidade igual de desperdiçar água ou perder colheita.

Este estudo tem as grandes limitações de não ter tido em conta o impacto das alterações climáticas e de usar dados com algumas décadas; para uma mais correcta avaliação esses factores deviam ser analisados e incorporados.

Como nota final, após todo o trabalho realizado e olhando para trás, a escolha do mês de Dezembro por ser o que apresentava a maior média de precipitação poderá ter sido uma opção errada. Apresenta a melhor média, mas tem uma variação maior (bem visível no diagrama de caixa). Essa variação implica uma maior amplitude de valores na simulação o que dificulta a tomada de decisões. Num próximo trabalho devia ser verificada a implementação usando o mês de Janeiro que apresenta uma média muito semelhante, mas com uma variação menor.

.

.

[1]  B. Vista, “Mudanças Climáticas E Mudanças Na Valoração Do Clima, Em Portugal, Nos Últimos 50 Anos,” Acta Geográfica, vol. 13, no. 33, pp. 196–208, 2019, doi: 10.5654/acta.v13i33.4882.
[2]  M. Belo-Pereira, E. Dutra, and P. Viterbo, “Evaluation of global precipitation data sets over the Iberian Peninsula,” J. Geophys. Res., vol. 116, no. D20, p. D20101, Oct. 2011, doi: 10.1029/2010JD015481.
[3]  H. Deng and H. Wickham, “Density Estimation In R,” Density Estim. R, no. September, p. 17, 2011.
[4]  “simukde package | R Documentation.” https://www.rdocumentation.org/packages/simukde/versions/1.2.0 (accessed Jan. 16, 2021).
[5]  M. L. Delignette-Muller and C. Dutang, “fitdistrplus : An R Package for Fitting Distributions,” J. Stat. Softw., vol. 64, no. 4, pp. 1–34, 2015, doi: 10.18637/jss.v064.i04.

.